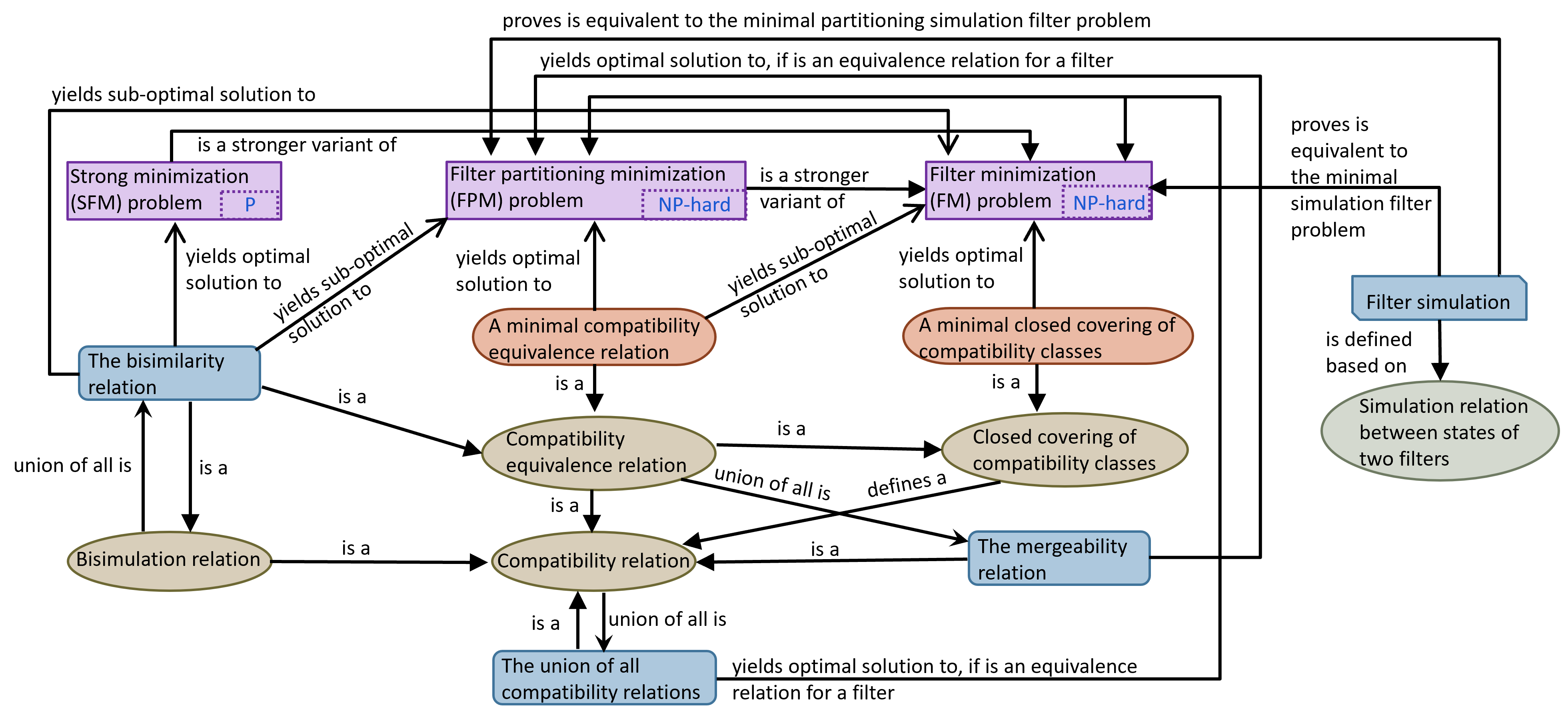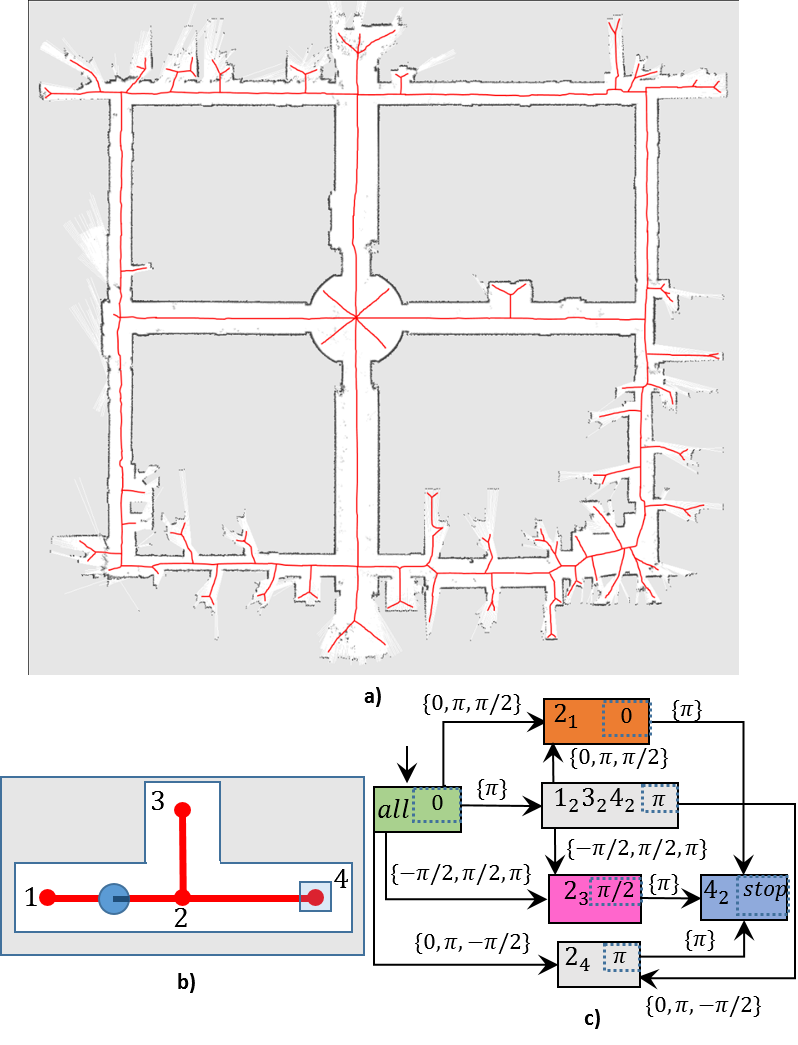
State space reduction of combinatorial filters

A map of the third floor of ACES building of University of Texas at Austin (P. Beeson, M. MacMahon, J. Modayil, A. Murarka, B. Kuipers, and B. Stankiewicz, "Integrating multiple representations of spatial knowl-edge for mapping, navigation, and communication." in Interaction Challenges for Intelligent Assistants, 2007, pp. 1-9.). The map is overlaid with the generalized Voronoi graph (GVG) of the environment in red. A simple environment and its GVG for illustrating how a combinatorial filter can be used as a plan to reach a goal location from full location uncertainty. A naively-constructed combinatorial filter, which the robot can use to navigate through the environment in part b) to reach point 3, starting from full location uncertainty.

Description

Combinatorial filters are formal structures for filtering and reasoning over discrete sensor data as well as for discrete planning. This project focuses on the combinatorial filter minimization problem, which is proved to be computationally hard. We study this problem and variant of through the lens of (bi)simulation, and show that the classical notion of bisimulation usually provides only sub-optimal solution to the problem. We introduce variants of bisimulation that are used to compute exact solution to the problem. We provide mathematical programming formulations that are used to compute exact and approximate solutions of the problem. We also identify several classes of filters for which the problem is solvable in polynomial time.

References

Hazhar Rahmani, Jason M. O'Kane. Equivalence notions for state space minimization of combinatorial filters. In IEEE Transactions on Robotics, 2021.
Yulin Zhang, Hazhar Rahmani, Dylan A. Shell, Jason M. O'Kane. Accelerating combinatorial filter reduction through constraints. In Proc. IEEE International Conference on Robotics and Automation, 2021.
Hazhar Rahmani, Jason M. O'Kane. Integer linear programming formulations of the filter partitioning minimization problem. Journal of Combinatorial Optimization, 2020.
Hazhar Rahmani, Jason M. O'Kane. On the relationship between bisimulation and combinatorial filter reduction. In Proc. IEEE International Conference on Robotics and Automation, 2018.

The connections between three problems related to filter reduction problems and the notions we provide to solve those problems. The main problem we study is FM, but we also study two stronger variants of it, FPM and SFM. FM and FPM are NP-hard, while SFM is in P. To solve FM and FPM, we introduce the notion of compatibility, which is a relaxed variant of bisimulation. The diagram shows the connection between this notion and optimal solutions to FM and FPM. In addition, it shows the connection between the notion of bisimulation to those three problems, while establishing a connection between the notion of simulation and those problems. It also shows three special relations, the bisimilarity relation, the union of all compatibility relations, and the mergeability relation.

Hazhar's home page